A fenti elnevezés gyakorlatilag a csúcsok azonosítása változó adatokon. Ezek az adatok változhatnak térben vagy időben. Jelen posztban csak a 2D csúcsok azonosítása a cél, de természetesen léteznek módszerek magasabb dimenziókra is.
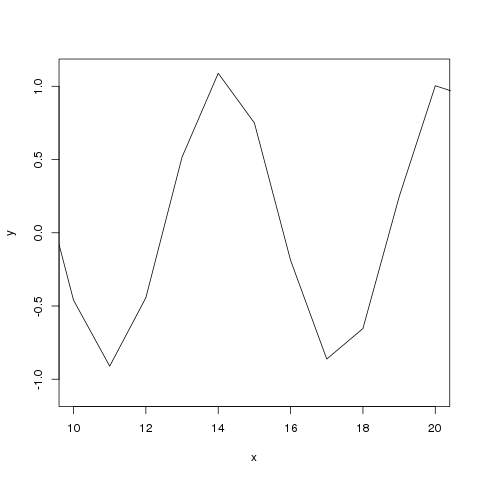
Aki egy kicsit is kutakodott a témában, bizonyára tapasztalta, hogy nincs egységes konszenzus, mit is nevezzünk csúcsnak. Amíg az első ábrán teljesen egyértelmű, mit tekintünk a legmagasabb pontnak, addig egy zajos, kiugró értékektől sem mentes adatnál már nem ilyen egyszerű a helyzet:
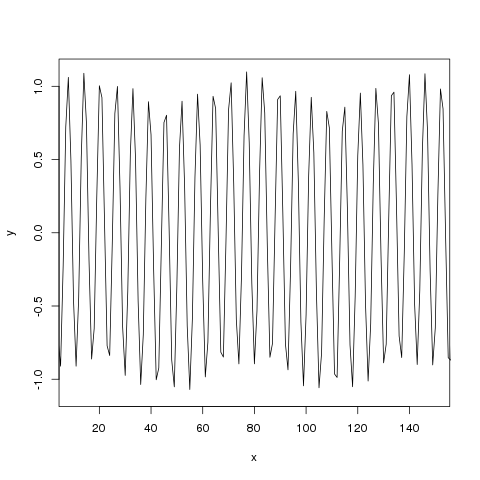
Talán ez is az oka, hogy a számtalan elérhető módszer mellett az emberek saját maguk is készítenek ad-hoc megoldásokat, amelyek ugyan úgy, vagy még jobban megfelelnek az igényeknek.
A következőkben azt mutatom meg, hogyan lehet minimális programozással, adott függvényekre támaszkodva megoldani a feladatot. Minimális programozás alatt azt értem, hogy csak a rendszer által biztosított függvényeket használjuk, semmilyen saját magunk által implementált adat transzformációt vagy algoritmust nem kell igénybe venni. Mintha előre gyártott LEGO elemeket illesztenénk össze, de saját kockákat nem gyártunk.
R
R-ben két csomag kerül bemutatásra. Az első a PeakPick. Használata rendkívül egyszerű. Bemenő paramétere egy oszlop mátrix. Ezt a matrix() függvénnyel állíthatjuk elő. Második paramétere a csúcspontok minimális távolsága.
peakPick(matrix(data, ncol=1), 100)
Visszatérési értéke egy logikai mátrix, a bemeneti adatokkal megegyező dimenzióval. Igaz érték esetén az adott elemet csúcspontként azonosította az algoritmus.
A második csomag a nem túl intuitív pracma néven fut. Bemenete egy vektor, tehár a PeakPick-el ellentétben csak 2D adatokra használhatjuk.
findpeaks(data)
A program viszonylag egyszerű algoritmust használ. Csúcsnak tekint mindent, ami előtt és mögött alacsonyabb értékek vannak. Az, hogy mennyi lépésen keresztül történjen ez a növekedés, az nups és ndown paraméterekkel szabályozható.
Python
Az adatelemzés másik nagyágyúja, a Python is biztosít lehetőséget lokális maximumok felderítésére. A scipy csomag jelfeldolgozó rutinok egész sorával rendelkezik.
import scipy.signal as sig
import numpy as np
sig.find_peaks_cwt(data, np.arange(5,10))
Ez a megoldás egy wavelet transzformáción alapul, visszatérési értéke a bemeneti adat indexei, ahol a csúcspontot sikerült megtalálni.
Összegzés
Én denzitás függvényeken próbáltam ki a módszereket és számomra úgy tűnt az R megoldásai sokkal jobb eredményt adtak, közelebb álltak ahhoz, amit én csúcspontnak tekintek. A Pythonos megoldása nagyon érzékeny a második paraméterre és ahogy különböző értékekekt adtam meg neki, néha nagyon meglepő eredményeket adott. Talán az is probléma volt, hogy nem vagyok túl járatos a wavelet transzformációban.
De az biztos, hogy lokális maximum keresésnél nem kerülhetjük el a bemenő adatok szűrését. Ez pedig tovább növeli a beállítandó paraméterek számát. Ezek alapján azt mondanám, hogy a csúcspontok megtalálása egyfajta próba-szerencse módszerrel történik, ahol minden esetben figyelembe kell venni a bemeneti adatok jellegét.