Trianguláció
A demóban több két dimenziós poligon lesz látható. Mivel szeretnénk rá textúrákat rakni OpenGL alatt, kénytelenek vagyunk felbontani őket háromszögekre. Minden sokszöget fel lehet bontani háromszögekre a matematikusok szerint, de a sokszög bonyuloltságától függően több algoritmust használhatunk. Mit jelent ez a gyakorlatban? A sokszöget alkotó csúcspontokat megadhatjuk véletlenszerűen, vagy szisztematikusan. A sokszög élei metszhetik egymást, tartalmazhatnak lyukakat, sőt a lyukak újabb lyukakat.
Egyszerűsíteni akartuk a munkánkat, ezért kikötöttük, hogy a sokszög nem tartalmazhat lyukakat, és a csúcsok sorrendje az óramutató járásával megegyező irányban írja le az alakzatot. A kikötések után az "ear clipping" (magyarul nem tudom, hogyan lehetne frappánsan lefordítani) algoritmusra esett a választás, amely kellően egyszerű ahhoz, hogy implementálni lehessen.
Az algoritmus leírása
Egy háromnál több csúcsot tartalmazó sokszög három egymás után következő csúcspontját összekötve háromszöget kapunk. Ez a háromszög lehet "száj" vagy "fül" attól függően, hogy a háromszög alapja a sokszögen belül vagy kívül található (1. ábra).
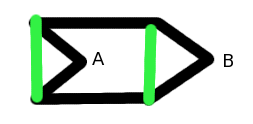
Az ábrán az A csúcs egy száj, míg a B egy fül. A fül eltávolításával egy egyszerűbb sokszöget kapunk. Addig ismételgetjük a fülek eltávolítását, amíg egy háromszög nem marad.
Egy háromszögről úgy döntjük el, hogy fül-e, hogy megvizsgáljuk a körüljárási irányukat. Erre van érdekes módon a háromszög területének kiszámításával kapunk választ.:
T = (x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1)
A fenti összefüggés ugyanis más előjelű eredményt ad a körüljárás irányától függően.
Egy lépés viszont még visszavan. Az ábrán látható sokszög elég egyszerű, de találkozhatunk olyan elvetemült esettel is, ahol egy másik csúcs a vizsgálandó háromszög területén belül található. Ilyen esetben nem szabad eltávolítani a csúcsot.
A kérdés eldöntésére a háromszög összes szomszédos csúcsával és a vizsgálandó ponttal alkotunk egy-egy háromszöget, és megvizsgáljuk ezen háromszöget körüljárását. Ha az összes körüljárási irány azonos, a pont az eredeti háromszögen belül található (2. ábra).
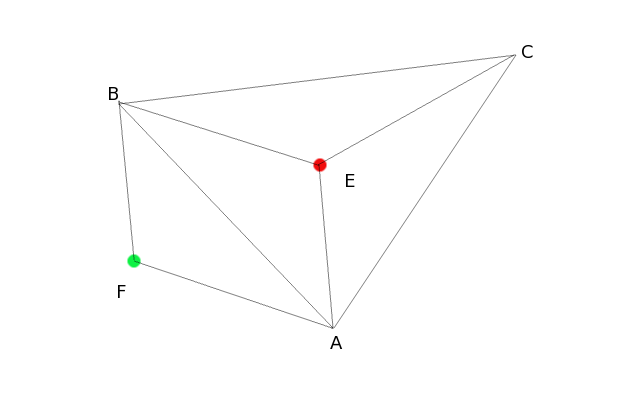Ha megvizsgáljuk az AEB és az AFB háromszögeket, láthatjuk, hogy más a körüljárási irányuk. Az algoritmus tesztelésére készítettem egy C#-os programot, ahova idővel további triangulációs algoritmusokat is be fogok építeni.
Források:
http://softsurfer.com/Archive/algorithm_0101/algorithm_0101.htm#Modern%20Triangles
http://www.gamedev.net/topic/295943-is-this-a-better-point-in-triangle-test-2d/
http://cgm.cs.mcgill.ca/~godfried/teaching/cg-projects/97/Ian/applet1.html
